This week’s Hammer of Math takes a look at some questions submitted by readers. Specifically we’ll look at the balance of flamers and ballistic skill, and the impact of abilities like automatic wounds or hits.
One of my goals for 2021 is to take a look at more reader-submitted questions. If you have an idea of something I should look at, please submit a request here. Please note that some questions work better for this column than others. Ideal questions are ones that have me take a look at the math behind a particular issue or question, suggest a comparison that would be applicable to a wide number of readers, or look at hypotheticals. And please note that the topic doesn’t necessarily have to be about Warhammer 40k; I’ll gladly look at other games as well!

Flamer vs Ballistic Skill
Our first question is from Robert Symons, who asks about the balance between flamers and weapons that require a successful hit roll.
At what point does the variable number of auto hits from a flamer work out better than Ballistic Skill abilities across factions? Also factoring in abilities to reroll number of shots, etc. For example, does a Terminator with 4 shots from a storm bolter land more hits than a flamer? Does that change with rerolling 1’s from a Captain nearby? Has this significantly changed with the increased range of the flamers?
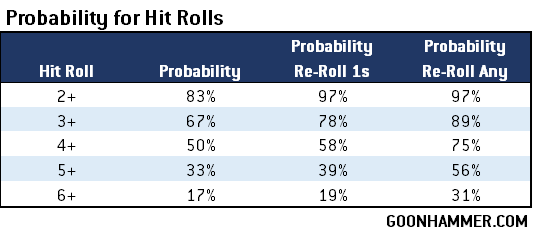
A typical flame weapon gets a random number (1d3, 1d6, 2d6, etc) of attacks that are guaranteed to hit. This makes it very helpful for Overwatch, or on units that may not necessarily have a great Ballistic Skill like Tyrannofexes. In order to do a comparison we can look at the expected value for the number of flamer hits and compare it to the expected value for the number of attacks that will hit for a given probability.
The formula we want to use is this:
Minimum # Attacks w/ BS = Average Flamer Hits / Probability of Hit
In other words the average number of attacks required to hit with a given roll is the average number of hits the flamer weapon deals divided by the probability of hitting. In the case of re-rolls we covered that the optimal strategy is to re-roll any result less than the average.
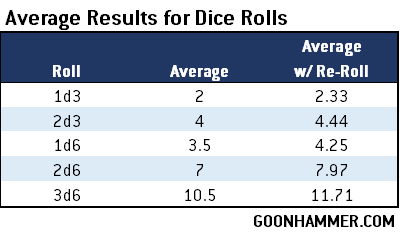
So for example if we take a look at a flamer dealing d6 hits out of a BS 3+ Space Marine then the average result is 3.5 and the probability of hitting is 67% then the resulting value is 5.2, which means that on average the Space Marine would need a weapon that dealt at least 6 attacks to average more hits than the flamer. In general flamer weapons are going to deal the most hits of any weapon available on a Datasheet, which is why they’re usually a lower range. One possible exception are Aggressors. The boltstorm gauntlet and fragstorm launcher deals 6 + d6 attacks with a hit roll, while the flamestorm gauntlets deal 2d6 flamer hits. The 2d6 flamer hits against a BS of 3+ result in a break even value of 10.44. The fragstorm launcher has the Blast trait which means it averages more attacks against larger units. Against units of 5 or less it averages 3.5 hits (regular 1d6), against units of 6-10 it averages 4 hits (1d6 minimum 3), and units of 11+ it’s guaranteed maximum hits. This means that assuming no BS modifiers the boltstorm option is actually more lethal than the flamestorm option against units of 11 or models, even though it has more range.
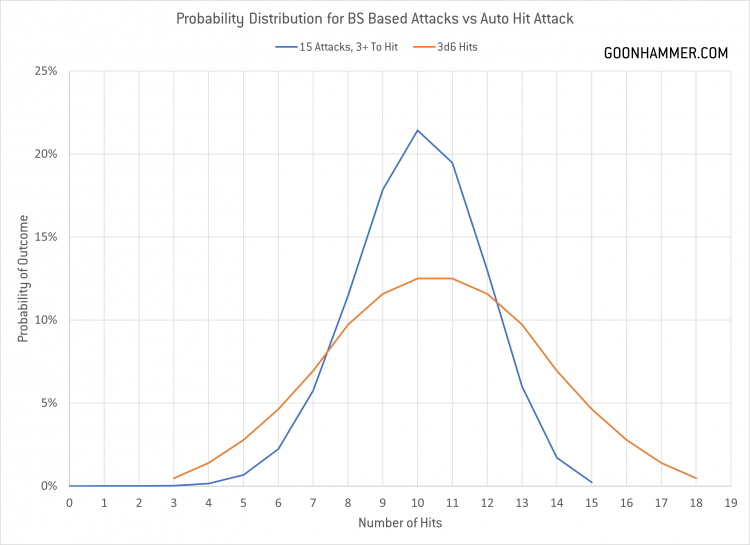
The other thing to consider is the probability curve. Take two attacks; 3d6 auto-hit attacks and then 15 attacks with a 3+ to hit. On average the 3d6 hits are better; 10.5 versus the average of 10 hits for the BS based attack. The difference is in the distribution; you’re less likely to see extreme values with a BS based attack.

Impact of Automatic Wounds
Our second question comes from reader Tim:
What is the math on abilities such as ‘automatically wounding on hit rolls of 6’ and how does that change based on things like the number of attacks/shots, the hit roll, wound roll, re-rolls, etc?”
When a unit gets an ability that allows it to bypass a wound, the end result is a fixed modification to the probability that’s similar to the impact of a re-roll. For this one we’ll need to go back to the probability chain for a given attack.
P(Damage) = P(Hit) * P(Wound) * [1 – P(Save)] * [1 – P(FNP)]
With the ability to automatically wound on an unmodified roll of 6 we now have a 17% chance to effectively set the probability of wounding to 1 for that particular attack. In order to calculate the effect we have to split the probability tree into three outcomes based on the hit roll. The first is the probability that a six will be rolled on the hit roll and automatically wound, which is a flat 1/6. The second is the probability that the attack will miss and therefore not wound, which is simply the inverse of the hit probability. The third outcome is the probability that the hit roll is neither a six nor a miss, which is then multiplied by the probability of wounding.
P(Damage w/ Auto-Wound on 6) = (1/6) + P(Hit, not 6) * P(Wound)
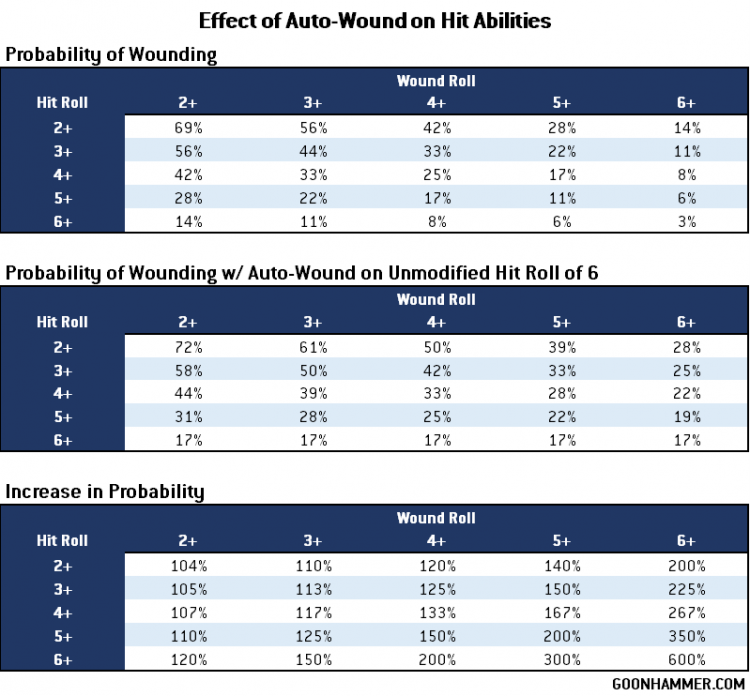
For example if I have a 3+ to hit and 4+ to wound then normally the chance of forcing the target to make a save is 33%. If I auto-wound on 6 then the probability of hitting but not getting a 6 (so a 3, 4, or 5) is 50%, which when multiplied by the 50% chance to wound results in a 25% probability. Add the 17% probability for getting a 6 (and therefore automatically wounding) and the net result is a 42% chance to wound, or a 125% improvement in the probability. The worse the hit or wound roll, the greater the impact of this ability. The chart below shows the result for all the possible combinations of hit and wound rolls. Note that this effect is independent of the number of shots, but re-rolls to hit would have a compounding effect since they increase the chance of getting an unmodified 6.
Thanks for reading! If you have any feedback, feel free to drop a note in the comments below or email us at contact@goonhammer.com. If you have any questions that you would like answered in a future article like this one, please submit them here.


